Driehoeken snijden uit vierkanten, deel 2
Half Square Triangles
Een pdf van dit blogbericht kun je HIER vinden, om dit op je eigen pc te bewaren of uit te printen.
Hoi, hier ben ik weer, Gerie. Met het langverwachte tweede deel van het uitrekenen van driehoeken, nu specifiek voor de Half Square Triangles (HST). Een HST is een vierkant, dat bestaat uit twee verschillend gekleurde, even grote driehoeken.
In deel 1 (Driehoeken snijden uit vierkanten) vertelde ik hoe ik worstelde met het feit dat ik nergens kon vinden hoe je uit kunt rekenen hoe groot de begin vierkanten moeten zijn, als je HST’s wilt maken die met een bepaald formaat in een blok moeten komen. Neem bijvoorbeeld dit blok.
Ik wil de hele maat van het blok in 12 inches. En er zitten drie formaten HST’s in. Toch lastig. Ik zal jullie niet weer bezighouden met een heel lang verhaal, hier komen gewoon de berekeningen, met snij wijzes. Laat je niet afschrikken door de rekentekens, je hoeft niet te weten wat ze betekenen of wat ze doen, het is gewoon een knopje op je rekenmachine. Of op de rekenmachine van je telefoon. Niet moeilijk, gewoon drukken.
Het probleem met mijn HST’s was dat er in de berekeningen van de vorige keer wel rekening gehouden werd met de naadtoeslagen, die er door het snijden bij kwamen, maar niet met de hoeveelheid stof. Als ik van 2 begin vierkanten, 8 HST vierkanten maak, worden ze kleiner. Logisch. Als ik twee taarten in acht stukken snijdt, worden de stukken ook kleiner dan de oorspronkelijke twee taarten. Dus ik moest zorgen dat er meer stof in de berekening kwam, meer oppervlakte, dus. Gelukkig wist mijn jongste zoon hoe dat moest. Hij zei: “De berekening die nog wel klopt met de hoeveelheid stof, die moet je gewoon ‘keer wortel 2’ doen”. ?????????????? Ja, dat gevoel had ik ook, geeft niks. Gewoon stap voor stap op de knopjes drukken. De berekening waar het nog klopte, was die voor twee driehoeken uit een vierkant. Dat is dezelfde berekening als voor twee HST’s uit twee vierkanten. Ik neem weer een voorbeeld vierkant van 10×10 centimeter. Dat betekent, dat ik in mijn blok een HST wil van 10×10 centimeter, als het blok af is.
De berekening is dan:
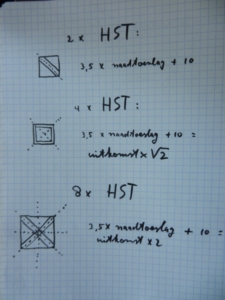
Twee HST’s tegelijkertijd:
3,5 x de naadtoeslag + 10.
Ik gebruik als naadtoeslag 0,75 centimeter, de uitslag van mijn som wordt dan: 3,5 x 0,75 = 2,625 en 2,625 + 10 = 12,625. Dat rond ik af naar 12,5 cm. De beginvierkanten knip of snijd je dus op 12,5 cm.
Je legt de vierkanten met de goede kanten op elkaar. Je tekent een diagonaal op het bovenste vierkant. Je naait aan beide kanten van die diagonaal je naadtoeslag (van 0,75 cm). Je knipt of snijdt over de getekende diagonaal en voilà: twee HST’s.
Daarna wel even precies op maat snijden. Soms hoeft er niets af, soms een heel klein dun draadje.
Maar nu heb ik een patroon waar ik 4 van die HST’s kan gebruiken. Dan moet ik de uitslag van de som van daarnet, namelijk: “12,265” vermenigvuldigen met wortel2, dat ziet er zo uit op een rekenmachine: √
dit teken heet wortel. Daar druk je eerst op, daarna druk je op de 2.
Niks engs aan, gewoon knopje voor knopje indrukken: 12,625 x √2 = 17,854. Dat rond ik af naar boven, 18 cm. Je knipt of snijdt twee vierkanten van 18×18 cm, legt ze met de goede kanten op elkaar en naait ze rondom op elkaar, met 0,75cm naadtoeslag. “Helemaal rondom dichtnaaien? Dan kun je het niet meer keren”. Klopt. Toch doen. Dan teken je op het bovenste vierkant twee diagonalen.
Je ziet op de foto dat ik met 1 diagonaal niet goed uitkom in de hoeken. Waarschijnlijk is de naadtoeslag niet helemaal goed, of was mijn begin vierkant niet helemaal vierkant. Op de foto heb ik de diagonaal getekend vanuit de hoeken van de stof, maar het is beter om dit vanuit de hoeken van de naadtoeslag te doen. Dan blijven de puntjes strakker. Ik ga uiteindelijk de HST’s toch nog op maat snijden, dus komt het meestal wel goed.
Je knipt of snijdt over beide getekende lijnen. Als je snijdt met een liniaal, hoef je niet eerst te tekenen, dan kun je gelijk de diagonalen snijden, als je liniaal lang genoeg is. Je vouwt de driehoeken open en voilà, vier HST’s. Daarna wel even precies op maat snijden. Soms hoeft er niets af, soms een heel klein dun draadje.
Vier HST’s tegelijkertijd:
3,5 x de naadtoeslag + 10. Uitkomst x √2
En het kan nog leuker. Je kan ook 8 HST’s tegelijkertijd maken. Dan heb je dezelfde som als daarnet, en die uitslag doe je weer x √2. Maar omdat √2 x √2 gewoon 2 is, is die som:
Acht HST’s tegelijkertijd:
3,5 x de naadtoeslag + 10. Uitkomst x 2.
Dus dat worden beginvierkanten van 3,5 x 0,75 = 2,625. En 2,625 + 10 = 12,625. En 12.625 x 2 =25,25 cm. Dat rond ik af naar 25,5 cm. Je snijdt 2 vierkanten van 25,5. Je legt ze met de goede kanten op elkaar. Je tekent twee diagonalen. Je naait aan beide zijden van beide diagonalen een naadtoeslag (0,75cm). Je tekent twee gewone kruisen horizontaal en verticaal in het midden van het bovenste vierkant.
Daarna knip of snijd je over de getekende lijnen, dus de diagonalen, horizontaal en vertikaal. Alle dingetjes openvouwen en voilà: 8 HST’s. Daarna wel even precies op maat snijden. Soms hoeft er niets af, soms een heel klein dun draadje.
Nog even alle berekeningen (formules) bij elkaar:
Heel veel plezier ermee, groetjes, Gerie.











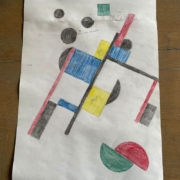




Bedankt Gerie, wat een goede manier, die ga ik zeker proberen! tot nu toe deed ik het altijd van strips, Bonnie Hunter heeft op haar quiltville website er een goede uitleg over, die zijn altijd een halve inch groter dan de HST uiteindelijk wordt, als je die nog niet kent is ook de moeite waard, maar daar gebruik ik wel de Half square triangle lineaal bij, dus die moet je dan net wel weer hebben…..
Hoi Hannah, veel plezier met uitproberen. Ik ken die methode van een halve inch groter wel maar ik wil zo min mogelijk stof wegsnijden. En ik heb die liniaal niet ;-). Groetjes, Gerie.